The balls into bins problem is a classic problem in probability theory that has many applications in computer science. It aims to answer how to balanced allocate resources in a random way. In this article, we will introduce the basic knowledge about this problem, and show its application in hashing.
Balls into Bins Problem
We have \(n\) balls and \(n\) bins. Each ball is assigned to a bin independently and uiformly at random. Define the load of bin \(i\) to be
\[L(i) = \text{number of balls assigned to bin } i\]Define the max load to be
\[\text{max-load} = \max_{i}{L(i)}.\]We would like to know how large \(\text{max-load}\) is with high probability. This is given by the following lemma.
(Lemma) With probability \(1-o(1)\), it holds
\[\text{max-load} = (1+o(1))\frac{\log{n}}{\log{\log{n}}}.\]In the rest of this section, we shall prove a weaker version: with probability \(1-\frac{1}{n}\), it holds
\[\text{max-load} \leq \frac{3\log{n}}{\log{\log{n}}}.\]Proof. For all bin \(i\), for any \(s\), we have
\[\begin{split} \Pr(L(i) \geq s) &\leq C_{n}^{s} \cdot (\frac{1}{n})^s \quad \quad \quad (\text{Union bound}) \\ &\leq (\frac{en}{s})^s \cdot (\frac{1}{n})^s \quad \quad (C_{n}^{s} \leq (\frac{en}{s})^s) \\ &= (\frac{e}{s})^s\\ &= \exp(-s(\log{s}-1)) \end{split}\]Now take
\[s = \frac{3\log{n}}{\log{\log{n}}}.\]We have
\[\log{s}-1 = \log{\log{n}} - \log{\log{\log{n}}} + \log{3} - 1 = (1-o(1))\log{\log{n}}.\]Therefore,
\[s(\log{s}-1) \geq 2\log{n}.\]It follows that
\[\Pr(L(i) \geq \frac{3\log{n}}{\log{\log{n}}}) \leq \frac{1}{n^2},\]and the union bound yields
\[\Pr(\text{max-load} \geq \frac{3\log{n}}{\log{\log{n}}}) \leq \frac{1}{n},\]as claimed.
Power of Two Choices
Now we want to figure out if there is a way to reduce the max load when randomly assign balls to bins.
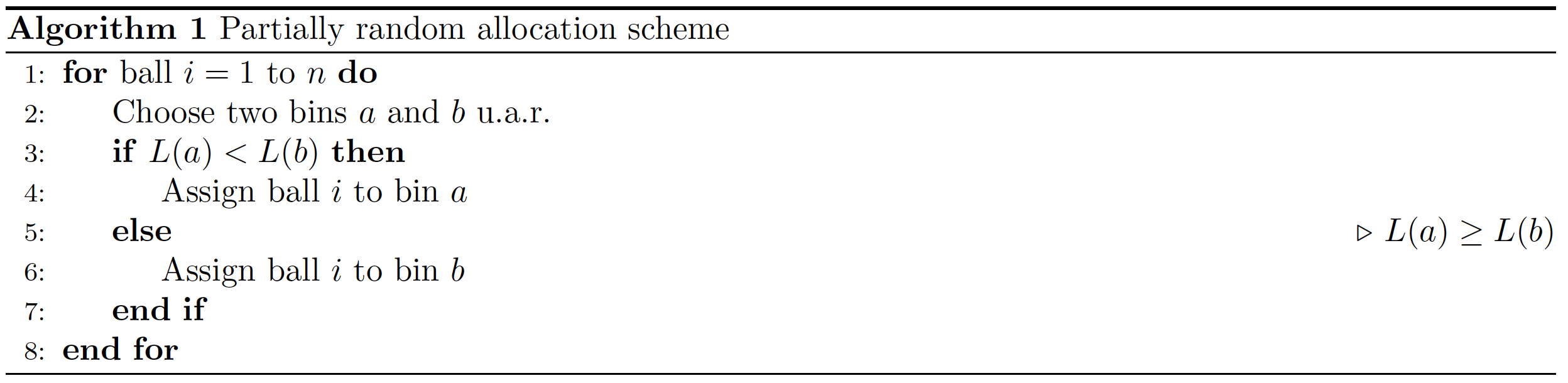
One idea is that instead of picking one random bin, we can pick two bins uniformly at random and place the ball into the bin with fewer balls. Following this strategym the max load turns out to be much smaller. This paradigm is known as the power of two random choices.
In other words, we assign each ball to the less loaded of two randomly chosen bins.
(Theorem) With probability \(1-O(\frac{\log^2{n}}{n})\), it holds
\[\text{max-load} = O(\log{\log{n}}).\]More generally, with \(d \geq 2\) choices, with high probability it holds
\[\text{max-load} = O(\frac{\log{\log{n}}}{\log{d}}).\]Application in Hashing
Consider a hash table in which all keys mapped to the same location are stored in a linked list. The effciency of accessing a key depends on the length of its list.
If we use a single hash function (which selects locations uniformly at random), then with high probability the longest list has size \(O(\frac{\log{n}}{\log{\log{n}}})\).
If we use two hash functions and put each new key in the shorter of the two lists, then with high probability the longest list has size \(O(\log{\log{n}})\).