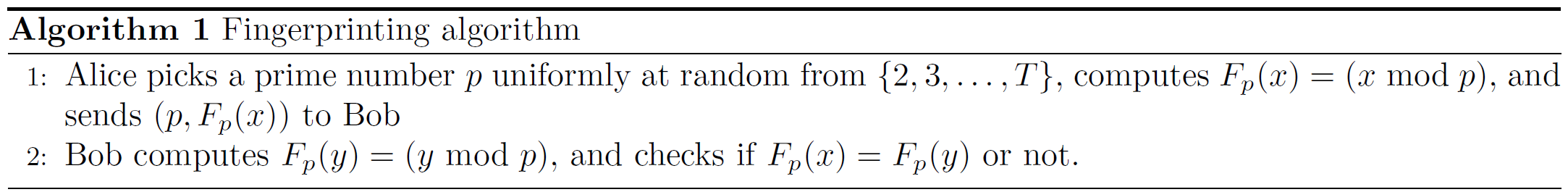In computer science, fingerprinting is a procedure that maps an arbitrarily large data item (such as a computer file) to a much shorter bit string, its fingerprint, that uniquely identifies the original data.
In this article, we will discuss a simple fingerprinting algorithm, and introduce a variant of it to solve the pattern matching problem.
Fingerprinting Algorithm
Suppose there are two people in the communication — Alice and Bob. They want to make sure that their respective data is the same.
Formally put, Alice has an \(n\)-bit number \(x = x_1x_2...x_n\). Bob also has an \(n\)-bit number \(y = y_1y_2...y_n\). Their goal is to check if \(x=y\) or not effciently, in the sense of low communication complexity.
Below is a simple fingerprinting algorithm.
The notation \(\text{mod}\) represents the modulo operation. Given two positive numbers \(x\) and \(p\), \(x \text{ mod } p\) is the remainder of the Euclidean division of \(p\) by \(x\).
For example, the expression “5 mod 2” evaluates to 1, and “9 mod 3” would evaluate to 0.
Observe that if \(x=y\), then \(F_p(x) = F_p(y)\) for any choice of \(p\), and Algorithm 1 outputs Yes always.
But if \(x \neq y\), we have to show that \(\Pr(F_p(x) \neq F_p(y)) \geq 1/2\) for a suitable choice of \(T\).
Here comes a key lemma. (proof is at the end of this article.)
(Lemma) Suppose \(T = 8n\). If \(x \neq y\), then
\[\Pr(F_p(x) = F_p(y)) \leq \frac{1}{2}.\]So, by the above lemma, we choose \(T = O(n)\), then \(p\) and \(F_p(x)\) have \(\log{n}\) bits. Therefore, in Algorithm 1, Alice only needs to send \(O(\log{n})\) bits to Bob.
The idea in our fingerprinting algorithm can be used to improve the polynomial identity testing algorithm. Sometimes evaluating polynomials may result in huge numbers during calculation. In this case, we can use modulo a small prime number as in fingerprinting to reduce computational cost.
Pattern Matching
Given an \(n\)-bit string \(x=x_1...x_n\) and a shorter \(m\)-bit string \(y=y_1...y_n\) where \(m \leq n\), check if \(y\) occurs as a substring of \(x\) or not. In other words, for each \(j\) let \(w(j)=x_j x_{j+1}...x_{j-m+1}\), and we want to check if there exists \(j\) such that \(w(j) = y\).
This is just a slightly modified version of the fingerprinting algorithm. To ensure this algorithm output No when \(y\) is not a substring of \(x\) with probability as least \(1/2\), \(T\) should be set as \(8mn\). (Proof omitted.)
In the end, let’s consider the running time of this algorithm.
Since \(T = O(mn)\), the prime \(p\) has \(O(\log{mn}) = O(\log{n})\) bits. Computing \(F_p(y)\) takes \(O(m)\) time since \(y\) has \(m\) bits. Computing \(F_p(w(j))\) for all \(j\) can be done recursively:
\[\begin{split} w(j+1) &= 2w(j) + x_{j+m} - 2^mx_j \\ \Longrightarrow \quad F_p(w(j+1)) &= (2 F_p(w(j)) + x_{j+m} - F_p(2^m)x_j) \text{ mod } p \end{split}\]As a result, each iteration takes \(O(1)\) time (note that we can compute \(F_p(2^m) = (2^m \text{ mod } p)\) once for all). The total running time is \(O(n + m)\).
Proof
This section is optional to read.
In this section, we try to prove the lemma in the first section.
Here we need some knowledge of number theory to establish this lemma.
Prime Number Theorem:
Let \(\pi(x)\) be the number of prime numbers less than or equal to \(x\). Then it holds
\[\pi(x) \sim \frac{x}{\ln{x}}.\]The notation \(f \sim g\) means two functions are comparable. Namely, \(\lim_{x \rightarrow \infty} \frac{f(x)}{g(x)} = 1\).
Moreover, for \(x \geq 17\), it holds
\[\frac{x}{\ln{x}} \leq \pi(x) \leq \frac{1.26x}{\ln{x}}.\]Let \(p_n\) be the \(n\)th prime number. Then it holds
\[p_n \sim n \ln{n}.\]Let \(p\) denote prime numbers in the equation below, and it holds
\[\sum_{p\leq x} \ln{p} = \ln{\prod_{p \leq x}p} \sim x.\]
The lemma we want to prove says if \(T = 8n\) and \(x \neq y\), then
\[\Pr(F_p(x) = F_p(y)) \leq \frac{1}{2}.\]Observe that, \(F_p(x) = F_p(y)\) if and only if \(p \mid \lvert x-y \rvert\).
The symbol \(m \mid n\) means “\(m\) divides \(n\)”; and \(m \nmid n\) is its “not” version. For example, \(2 \mid 10\), but \(3 \nmid 10\). See this wiki page for more information.
We need to count the number of primes that divides \(\lvert x-y \rvert\), and we denote this count by \(k\).
Consider \(\lvert x-y \rvert\) has at most \(n\) bits, by the Prime Number Theorem, we can deduce \(p_k \leq n\) from
\[2^n \geq |x-y| \geq p_1...p_k \gtrsim e^{p_k} \geq 2^{p_k}.\]Notice that \(p_k \leq n\) is equivalent to \(\pi(n) \geq k\).
Therefore, we deduce again from the Prime Number Theorem that
\[\Pr(F_p(x) = F_p(y)) \leq \frac{\pi(n)}{\pi(T)} \leq \frac{2n/\log{n}}{T/\log{T}} = \frac{2n}{T} \cdot \frac{\log{T}}{\log{n}} \leq \frac{1}{4} \cdot 2 = \frac{1}{2},\]as wanted.